Macroeconomic simulations on a quantum computer via cloud – solving matrix problems

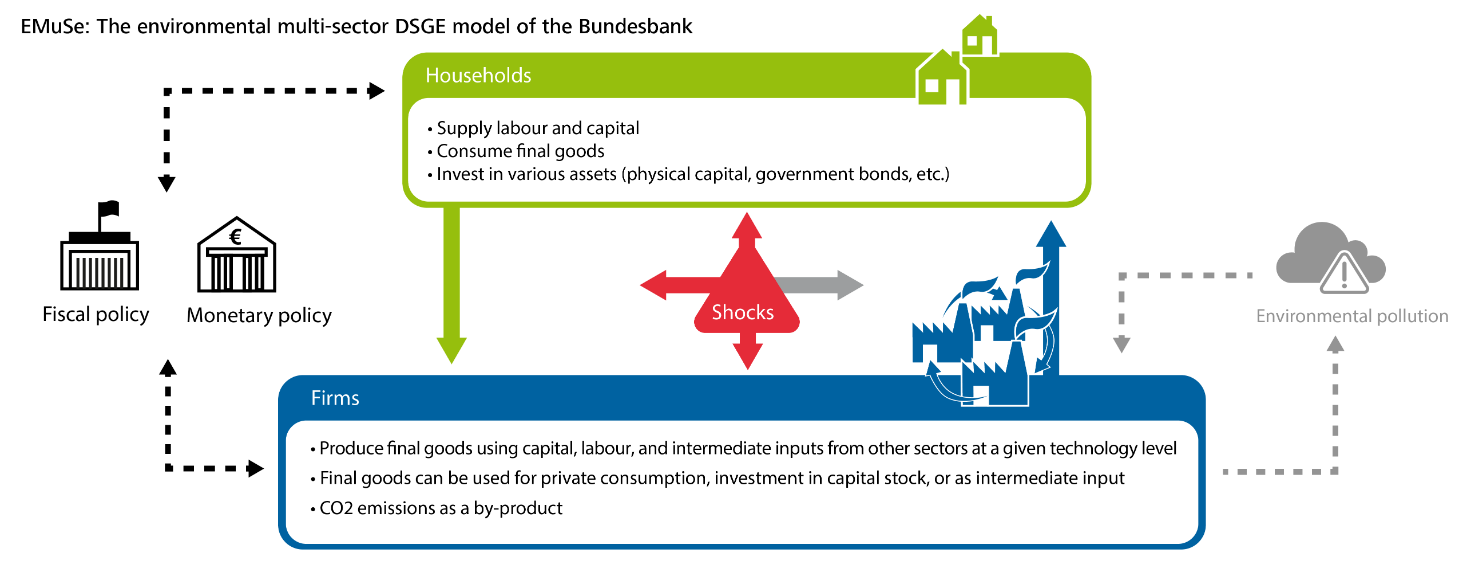
Macroeconomics refers to the study of the overall economy, focusing on broad issues like inflation, unemployment, economic growth, and the impact of government policies. Through the application of computational models, macroeconomic simulations explore the effects of various policies, shocks, and other key macroeconomic variables like GDP, inflation, and unemployment. These simulations provide a virtual laboratory where different economic scenarios can be tested to gain insight into how economies function. Even if the models used to generate these simulations are based on only a few equations involving a few variables, they can become extremely complex to the point of being intractable for classical computers. Quantum computers offer the potential to enable macroeconomic simulations with a previously inaccessible complexity by providing faster and more efficient solutions to these challenging models.

Our partners at JoS Quantum are investigating the use of quantum technology for macroeconomic simulations as part of their project MaQro with the Deutsche Bundesbank. As explained in one of their articles, the dynamic stochastic general equilibrium (DSGE) model—one of the most powerful tools used for forecasting—is largely based on the ability to solve linear systems of equations. Historically, quantum computers became well-known for their immense potential in solving systems of linear equations. One example is the Harrow-Hassidim-Loyd (HHL) algorithm, (Phys. Rev. Lett. vol. 15, no. 103, pp. 150502 (2009)), a powerful quantum algorithm that allows extracting the solution of a system of linear equations—potentially faster than any classical counterpart. This algorithm is built on quantum phase estimation, which serves as a subroutine to efficiently calculate the eigenvalues of the target matrix. The implementation of the HHL algorithm to solve systems of linear equations using a quantum computer represents one of the foundational steps toward enabling macroeconomic simulations on quantum computers.

In collaboration with JoS Quantum, we conducted a series of Proof of Concept (PoC) experiments on IBEX Q1, AQT’s quantum computer available through the cloud service, ARNICA.

We solved HHL algorithms of different complexity and showcase how to implement these calculations on AQT’s cloud ARNICA in a short video recorded by Lucas Euler.

To start, a simple case effectively illustrates how the algorithm can be solved on our hardware:

To solve this matrix the following quantum circuit, using four qubits, is required.

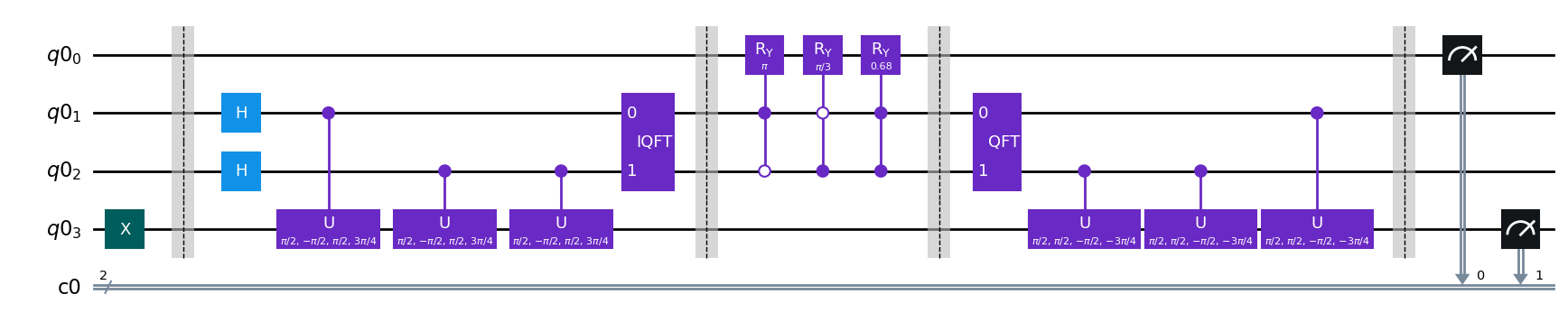
Figure 1: High-level abstraction of the implemented HHL algorithm.

Transpiled to AQT’s native gate operations, compatible with the architecture of IBEX Q1 quantum computer, the circuit reads:

Figure 2: Native gate representation of the implemented HHL algorithm.

It becomes clear that the HHL algorithm is particularly demanding in terms of the depth of the circuit (61 operations), rather than the number of qubits.

The results of the calculation are encoded in bin 1 and 3 of the following histogram:

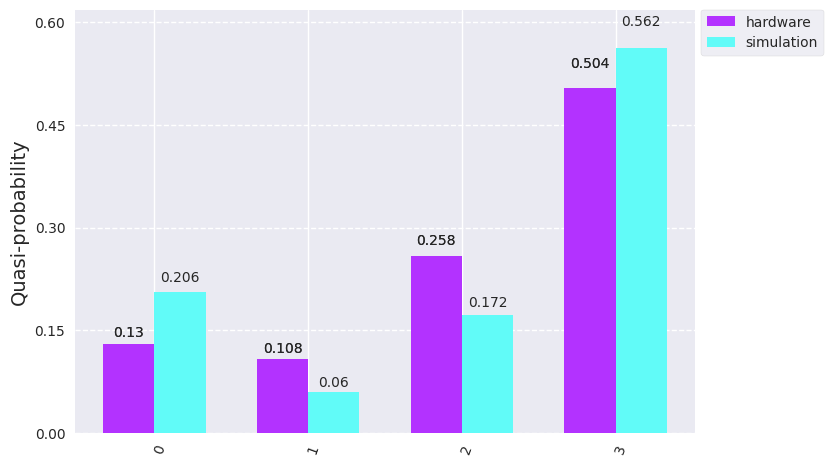
Figure 3: Comparison of hardware run and noise free simulations of the algorithm in figure 1.

The comparison of the hardware run in figure 3 and a simulation on an ideal, noise-free system, confirms, the results match the expected solution. In the case of our test matrix, the solution is represented by the ratio between bin 1 and 3. The video mentioned previously shows that also more complex problems can be successfully solved —proving that even with a limited amount of qubits, it is already possible to solve a varied set of linear equations.

In conclusion, we have shown that solving sets of linear equations using a quantum computer is in principle possible. Taking into account that the runtime of the quantum algorithm scales exponentially better than classical methods this marks an important step toward solving more complex macroeconomic models using quantum computers.

© Photocredits: AQT, Shutterstock