Quantum memory lifetime
In contrast to a classical computer where information is stored in binary states, a quantum computer can contain information in superpositions of quantum states specified by a relative phase and amplitude.
On today’s noisy intermediate-scale quantum computing (NISQ) systems, quantum states and their superposition can be fragile and susceptible to disturbances from the environment, leading to information loss and thus reduction in performance. The effect of this disturbance can be quantified by the lifetime of the quantum information stored in the qubits – referred to as memory lifetime.

The memory time is dominated by two effects that can be witnessed on qubits: the first, spontaneous decay describes an effect where one qubit state is changed to the other. The respective rate is described by the T1 time. The second results from information loss due to scrambling of the phase relation in the superposition state, which is described by the T2 time. Ideally, both the T1 and T2 time should be significantly longer than the time it takes to manipulate the qubits. For AQT’s quantum systems, the ratio is ~1000:1.
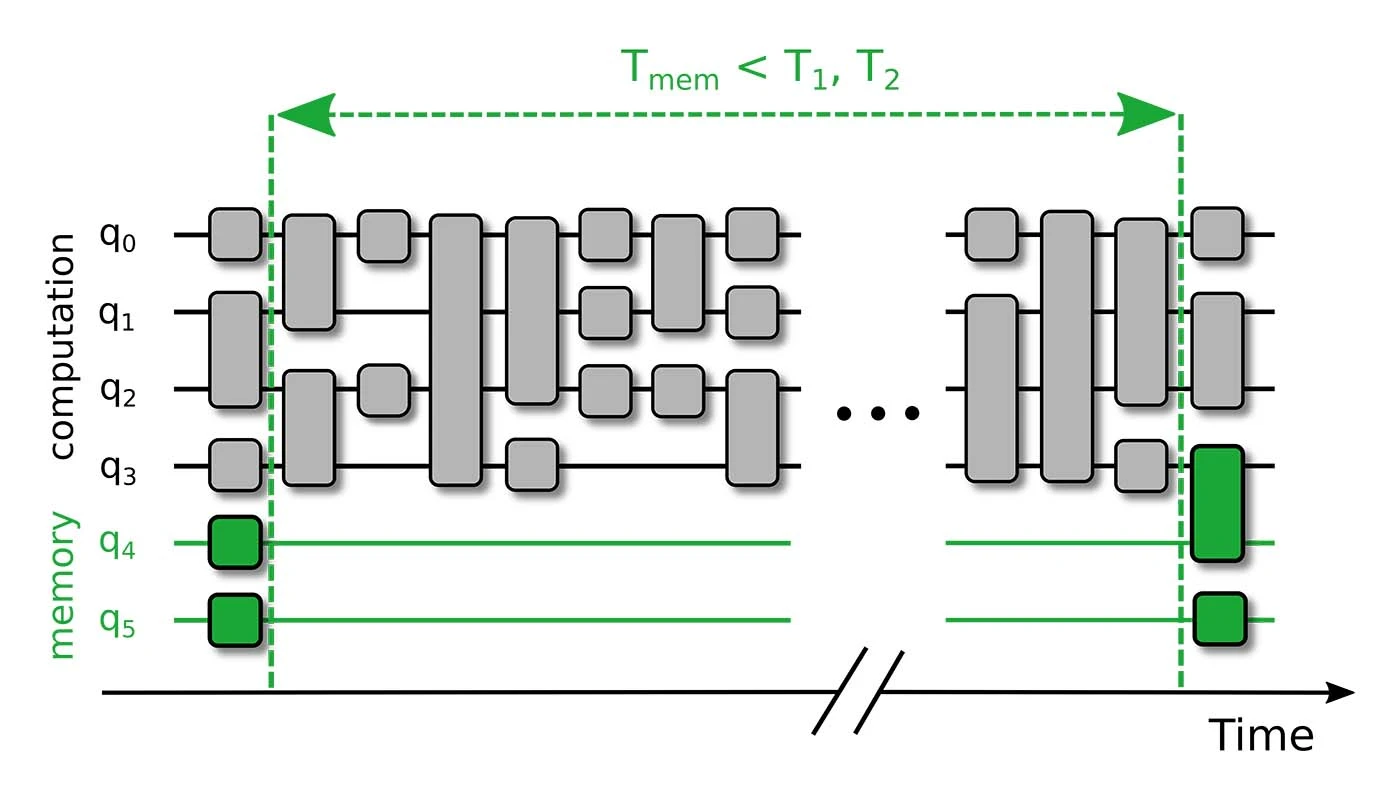
The T1 time in our systems describes the decay of qubit excitation resulting from energy exchange between an ion and its environment. The T1 time is limited by the natural lifetime of the energy levels constituting the qubit system. The T2 time, on the other hand, describes the loss of coherence of a quantum system resulting from dephasing induced predominantly by laser and magnetic field fluctuations.
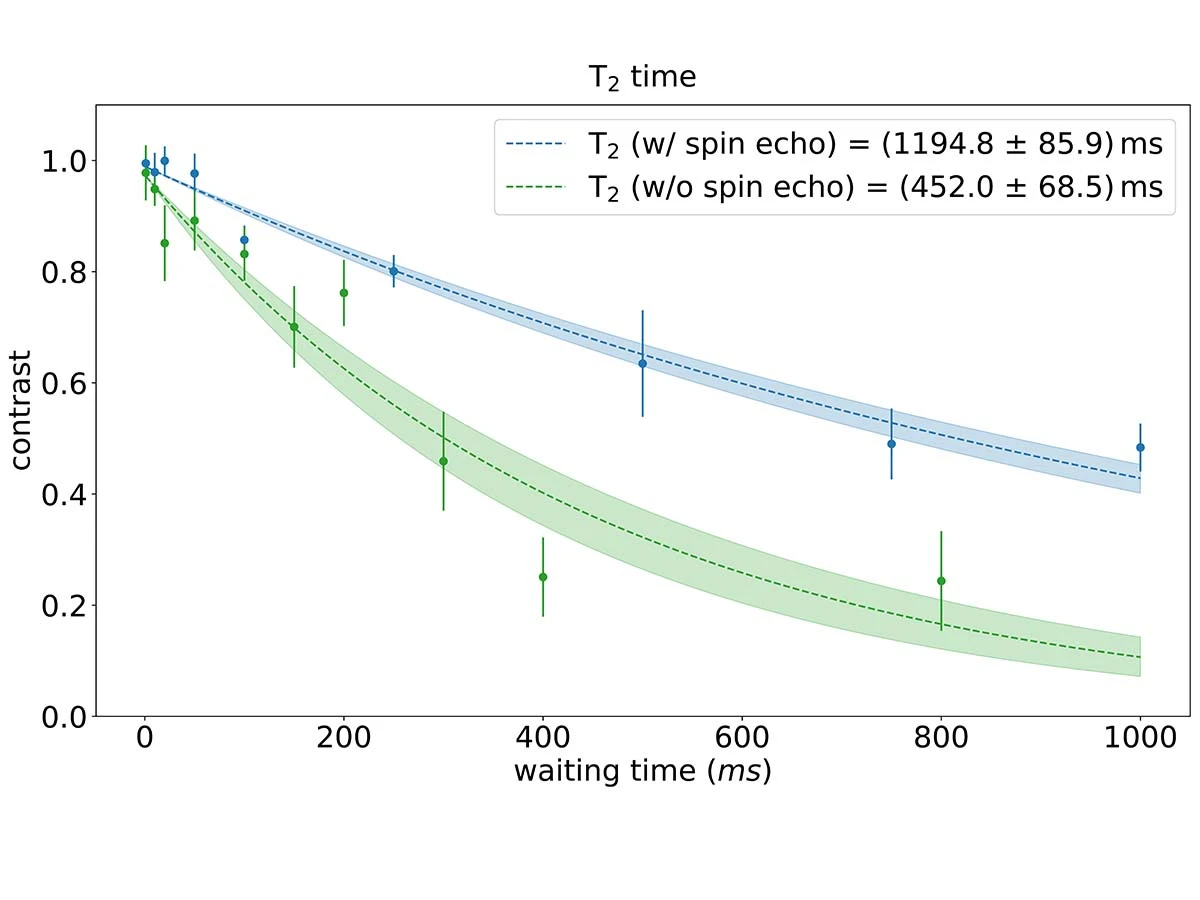
Physically, the ultimate limit for the T2 time of the quantum system is given by the lifetime T1 : T2 < 2*T1. In other words: a well isolated quantum system should demonstrate T2 times ‘on the order of’ T1. Here, we present the T1 and T2 time measured in the AQT MARMOT system. We first highlight the identical behaviour of each ion, exemplified by the time T1 = 1.14 +- 0.06 s, measured for each ion in a register of 20 ions. A laser linewidth of less than 1 Hz and highly stable magnetic fields provide us with an excellent T2 time between 0.5-1.2 s. Considering typical gate times on the order of 10 to 100 µs, the quantum memory persists for the equivalent of up to 1000 quantum gate operations – a feat highly challenging for other platforms.
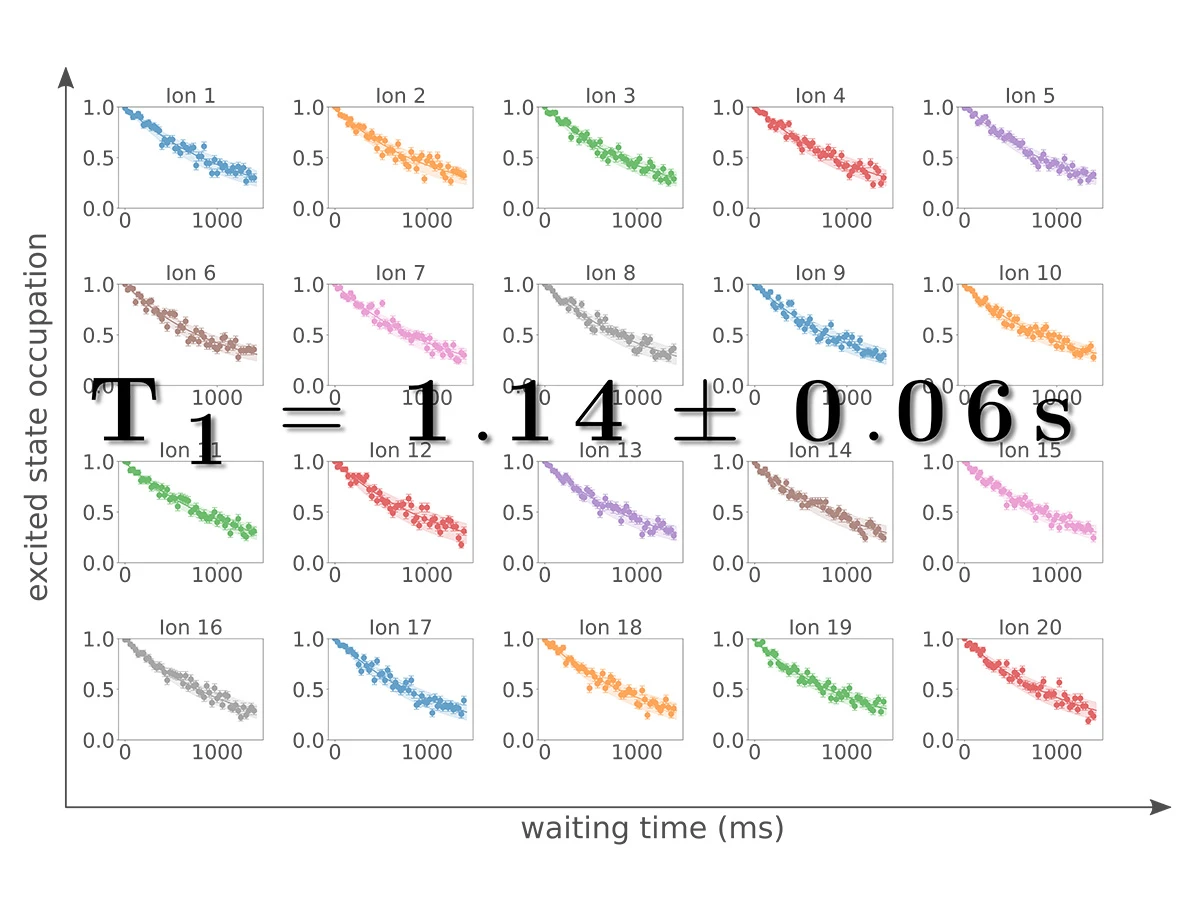
T1 time for a register of 20 qubits
All qubit lifetimes T1 from a register of 20 qubits presented in the figure match within one standard deviation and agree with the natural lifetime of the qubit transition T1,nat= 1.165 +- 0.011 s (A. Kreuter et al. PRA 71, 032504 (2005))
T2 time
T2 time of the qubit transition. The blue and green dots represent the measurement results derived from a standard Ramsey experiment and a Ramsey measurement with spin echo refocusing, respectively. We determine the T2 time by fitting exponential decays to the two experiments (see figure legend).

All qubits in an ion chain behave identically like twins
The identical nature of all qubits, in combination with low error rates and all-to-all connectivity, allow us to reduce circuit compilation and calibration overhead. This simplifies the implementation of quantum applications making the ion-based quantum processor a preferable platform for quantum computing.
Did you know?
Errors in quantum processors are one of the largest bottlenecks to the commercially beneficial implementation of quantum applications. While many entities claim to push for more and more qubits, the more challenging aspect is to at least maintain, but ideally significantly improve the performance of the quantum gate operations.
© Photocredits: Dieter Kühl
