Simulating turbulent flow – Aerospace prepares for quantum computing

The overall dominating metric in public communications on performance of quantum computer hardware is number of qubits. While scaling to higher number of qubits remains on the most prominent challenges for future quantum hardware, the importance of the ability to perform complex circuits of a depth which allows for testing real world use cases is often omitted.

The Hadamard test is a widely used routine in quantum computing to compute the real and imaginary part of expectation values of unitary operators. Here, we use a resource-efficient low-depth implementation scheme that adopts the Hadamard test construction, meaning that each unitary operation is controlled from the ancilla qubit and the controlled operations are sandwiched between two Hadamard gates applied to the ancilla qubit.

Efforts towards developing low-depth implementations of quantum circuits usually involve increasing the number of qubits to enable parallelization and reduce the circuit depth at the expense of the circuit width. Such methods are typically designed to achieve a favorable scaling of the overall depth width product compared to the widely used conventional Hadamard test implementations. However, it remains highly desirable to reduce the circuit depth without incurring an increase in circuit width, thereby enabling more resource-efficient implementations of Hadamard test circuits. We use an efficient realization of a broad class of Hadamard test quantum circuits, significantly reducing gate resource requirements.

The details of the tailored ansatz structure and the implementation in the nonlinear dynamics problem of Burgers’ equation can be found here: http://arxiv.org/abs/2507.19250. In the following we focus on the quantum gate resource requirements for the Burgers’ dynamics which arise from the ansatz.

We use the most demanding circuit in terms of both qubits count and two-qubit entangling operations from the detailed paper (https://arxiv.org/abs/2507.19250) to compare the quantum gate resource requirements of our low-depth scheme and the conventional implementation of Hadamard test circuits. Figure 5 highlights a substantial reduction in the two-qubit gate budget required to simulate Burgers’ dynamics with the low-depth scheme. Specifically, the two-qubit gate count g2 is reduced by roughly a factor of two to three on both superconducting and trapped ion hardware platforms, as shown in Fig. 1a and Fig. 1b, respectively. However, because of all-to-all qubit connectivity in the trapped-ion processor, they require a factor of 4,5 fewer two-qubit gates than their superconducting counterparts, rendering them a particularly favorable platform for executing the variational algorithm.

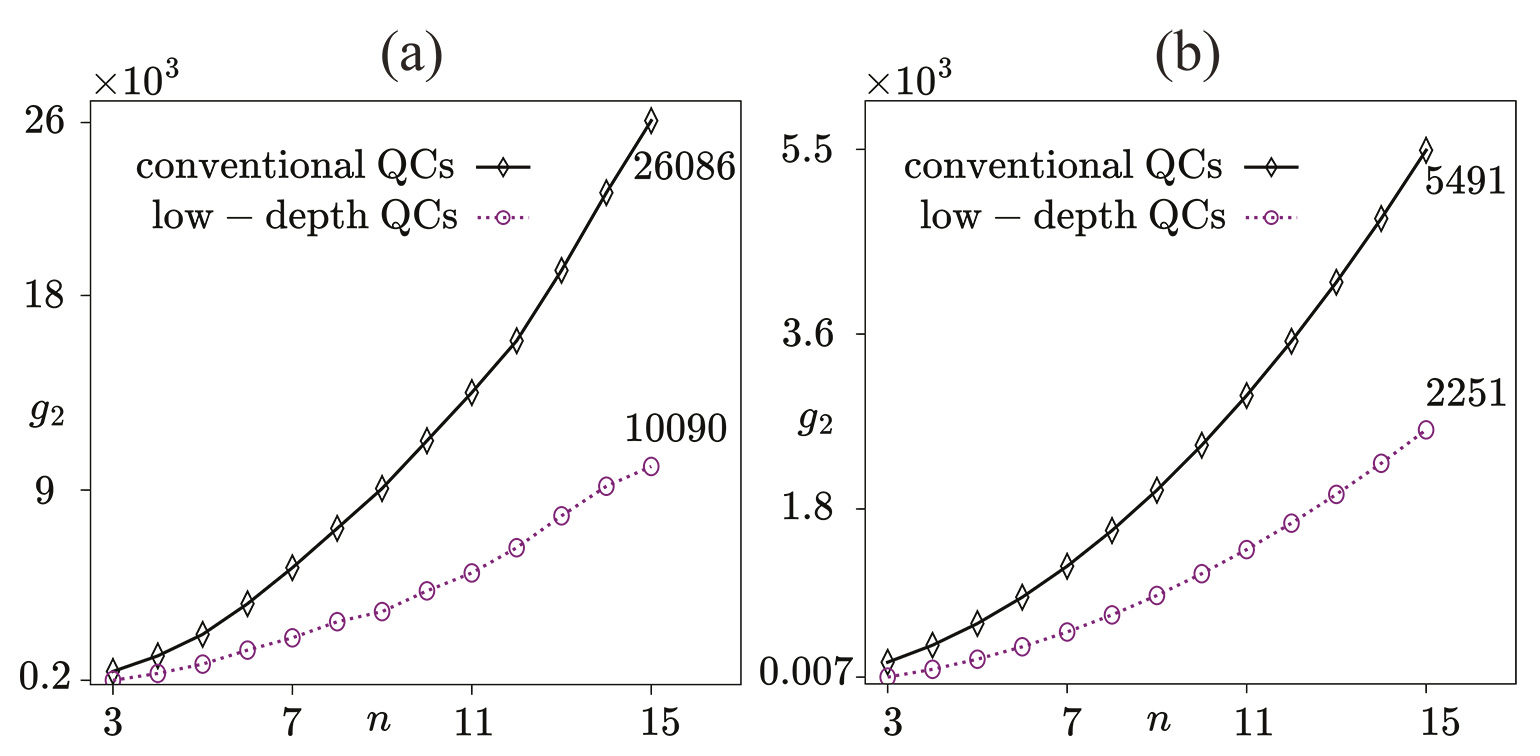
Figure 1: Comparison of two-qubit gate count g2 for conventional and low-depth Hadamard test QCs for Burgers’ dynamics. Panel a (b) shows the two-qubit gate count for superconducting (trapped-ion) based devices where black and purple colors indicate the gate count g2 for convectional and low-depth Hadamard test QCs.

We now compare the performance of different processors using simulations of Burgers’ dynamics of a 1D turbulent flow, with noise models derived from IBM’s Heron R2, Eagle R3 and AQT’s IBEX Q1. This assesses how the resource efficient low-depth Hadamard test construction enhances the feasibility of implementing the variational algorithm on different contemporary NISQ hardware devices.

Figure 2 shows the result of the noisy simulations for the IBM devices, a to c, and ATQ’s IBEX Q1 quantum processor, d to f. The blue curve indicates the exact classical solution of the 1D velocity profile (u(x)) of the turbulent flow while the orange curve represents the solution of the variational quantum algorithm with reduced depth.

For all three IBM devices the noisy simulations exhibit random behaviour offering no indication of physical significance already for the first time step at t = 0,2 of the dynamics. The overlap with the classical reference is remarkably low.

Owing to the all-to-all qubit connectivity of IBEX Q1, the low-depth scheme decreases the single- and two qubit gate counts more than a threefold leading to a gate count that is substantially lower than the one required on IBM processors. The corresponding noisy simulations yield encouraging results, as shown in Fig. 6d-6f, with very good overlaps between the variational and classical states at all three times steps t = 0.2, t = 0.4, and t = 0.6. Despite a slight decline in state fidelity, the characteristic turbulent-regime shockwave behavior (discontinuity) is already evident at t = 0.4, which becomes more pronounced at t = 0.6.

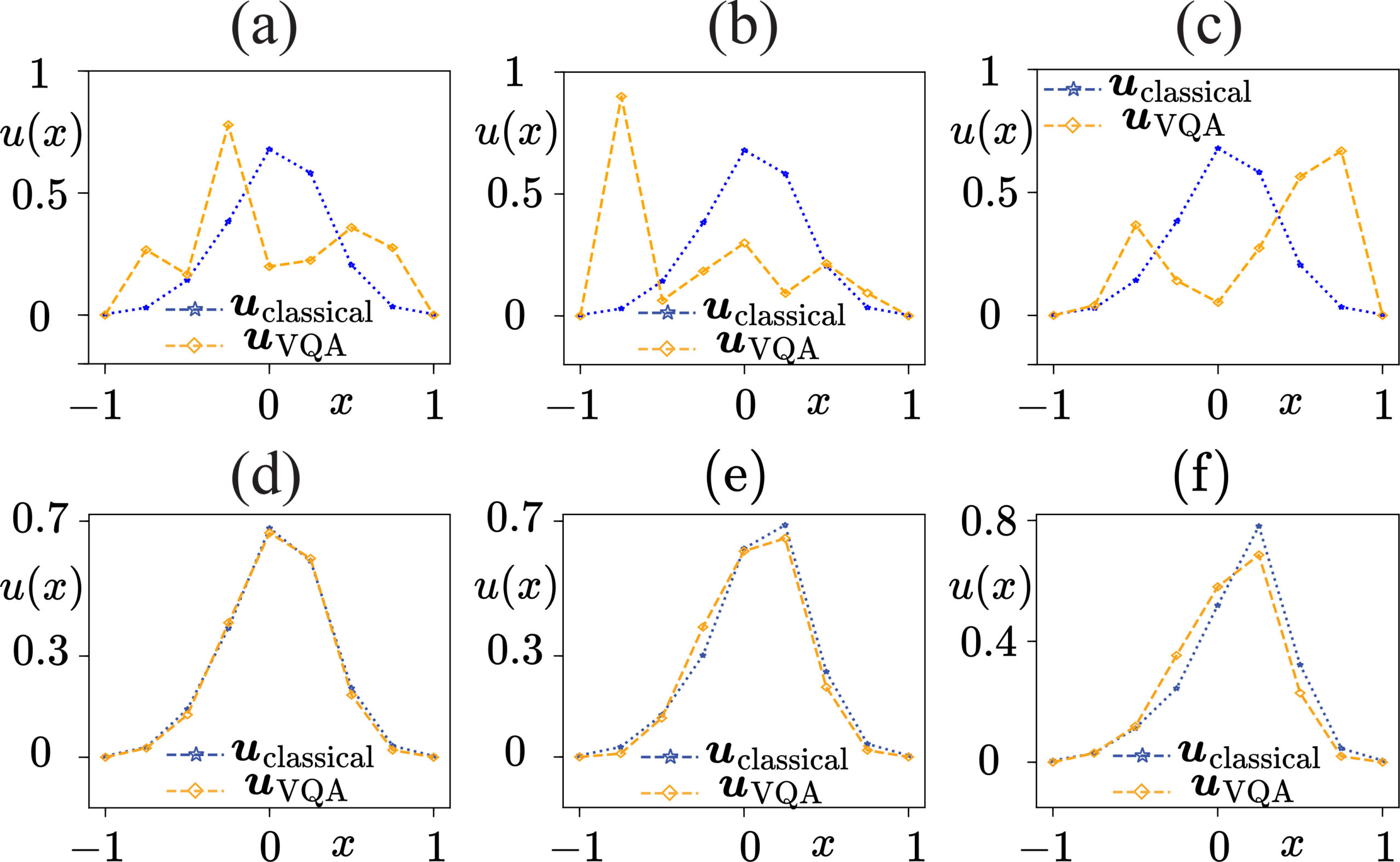
Figure 2: (a-c) Simulated fluid field profile at t = 0.2 in the presence of noise models derived from (a) ibm-brisbane (Eagle R3), (b) ibm-kingston (Heron R2), and (c) ibm-sherbrook (Eagle R3) devices. The velocity field uVQA has (a) 45.45%, (b) 16.63%, and (c) 19.26% fidelity with the classical simulation results uclassical. Panels (d-f) show the velocity field at (d) t = 0.2, (e) t = 0.4, and (f) t = 0.6 in the presence of noise model derived from AQT’s IBEXQ1 device. Here, the fidelity between the variational results uVQA and the classical results uclassical are (d) 99.87%, (e) 98.58%, and (f) 96.45%.

Real devices exhibit additional correlated effects compared to the limited number of noise channels of the available simulators, rendering the actual error landscape considerably more complex than the optimistic noise models. Therefore, we carry out demonstrations on AQT’s IBEX Q1 to crosscheck with a real device.

The hardware demonstration of the low-depth scheme on the AQT’s IBEX Q1 processor, featuring 12 fully connected qubits is shown in figure 3.  The Burgers’ dynamics for two consecutive time steps, advancing from t = 0 to t = 0.2, and subsequently from t = 0.2 to t = 0.4 can be simulated faithfully.  The variational algorithm prepares a quantum state exhibiting a 97.48% overlap with the classical velocity field at t = 0.2, and 95.66% at t = 0.4.

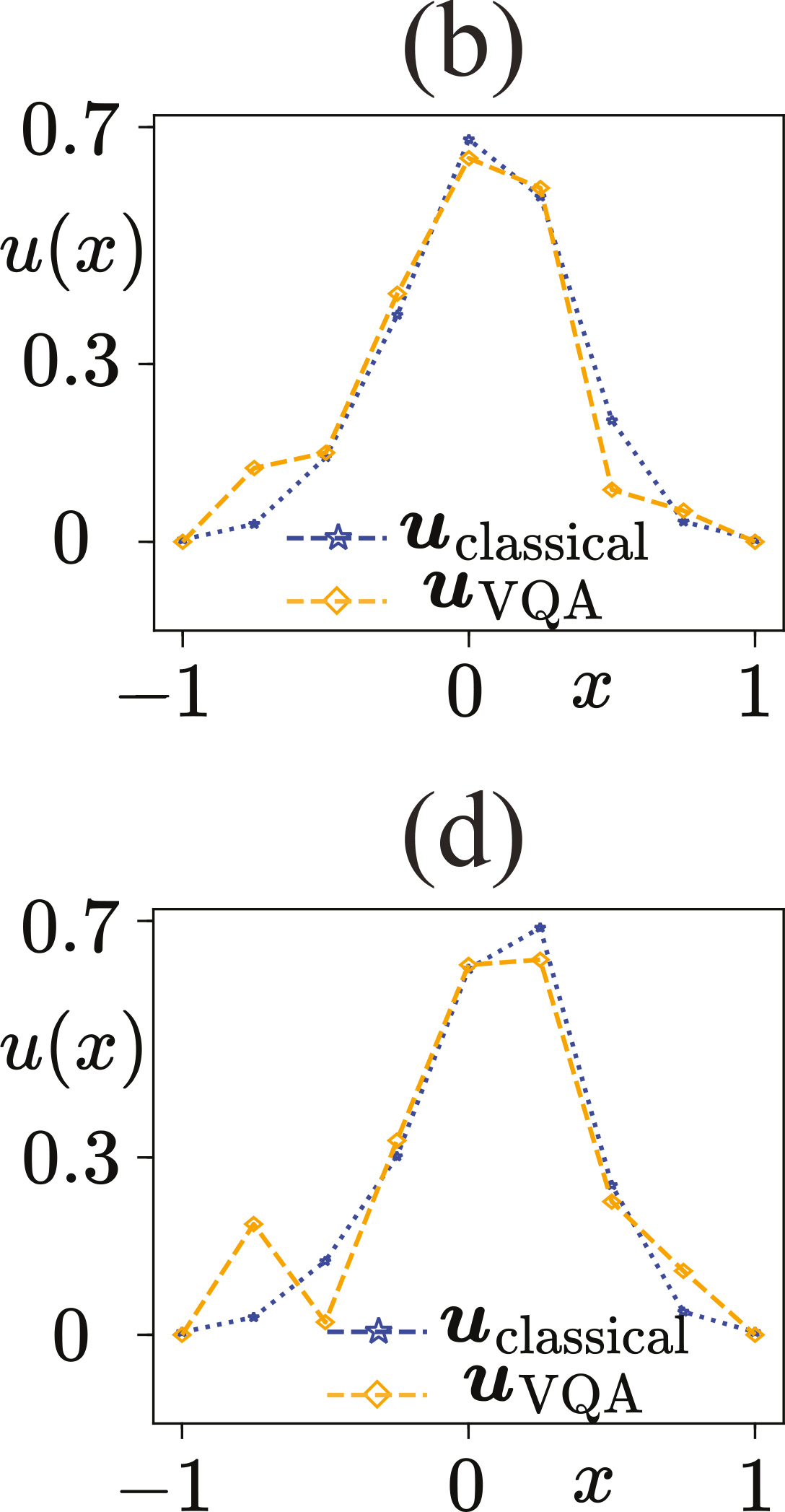
Figure 3: Results of the variational algorithm executed on AQT’s trapped-ion IBEX Q1 processor. Panel (b, d) illustrate the fluid velocity profile at (b) t = 0.2 with fidelity 97.48% and (d) t = 0.4 with fidelity 95.66%.

This represents the first observation of turbulent fluid dynamics on quantum hardware. The results highlight the power of AQT’s hardware, featuring high fidelity operation, long coherence times and full connectivity. In combination with the novel low-depth scheme (https://arxiv.org/abs/2507.19250), , this allows to faithfully simulate more complex problems and therefore encode the underlying physical phenomena more accurate than with any other qubit modality.

Acknowledgements:
Special thanks to Eleftherios Mastorakis, Muhammad Umer and Dimitris G. Angelakis. This work was supported by the EU HORIZON—Project 101080085 – QCFD and the National Research Foundation, Singapore through the National Quantum Office, hosted in A*STAR, under its Centre for Quantum Technologies Funding Initiative (S24Q2d0009), Quantum Engineering Program NRF2021-QEP2-02-P02. FR acknowledges support from HPQC, MILLENION, and QCDC.

© Photocredits: AQT, Shutterstock